简述

一般来说移动机器人的运动模型可分为完整约束和非完整约束。

完整约束可称为可积的Pfaffian约束，非完整约束可称为不可积的Pfaffian的约束，详细看《现代机器人学》的位形与速度约束。

• 完整约束（Holonomic，控制数=自由度）

  可以用一个由位形变量$x,y,\theta$​组成的方程（位置约束）来描述。包括全向轮模型

• 非完整约束（Non-holonomic，控制数<自由度）

  只能用位形变量的微分方程（速度约束）描述，无法积分成一个位形变量的约束方程。包括双轮自行车模型和差速模型

通常地面机器人的自由度为3，包括x,y与朝向。对于角轮（castor wheels）或者是全向轮（Omni-wheels）的机器人，是holonomic的，因为它能够朝各个方向移动，机器人的总自由度与可控自由度是相等的。

汽车模型可控的自由度为2，包括油门/刹车和方向盘转角，差速模型可控自由度为2，包括X方向和朝向（差速转向）。使得它难以满足任何方向的行驶（除非车辆发生打滑或侧滑），所以是非完整性约束。

相关概念

• 广义坐标：广义坐标是用来描述系统位形所需要的独立参数，或者最少参数。当分析有的问题时（尤其是当有许多约束条件的时候），尽量选择独立的广义坐标。因为这样可以减少代表约束的变量。
• 位形空间（configuration space，C-space）：所有位置形态集合。
• 任务空间（task space）：所有可能的机器人位姿构成的集合。

单轮模型（unicycle model）

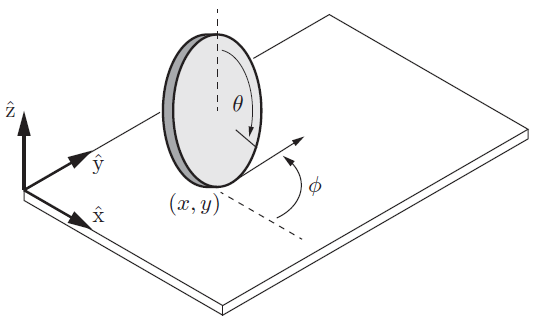
单轮模型的位形为$(\theta,x,y)$，$r$为车轮半径，$(x,y)$为车轮与地面接触点，$\phi$为前进方向，单轮的规范简化模型为

$$ \dot{q} = \begin{bmatrix} \dot{\phi} \\ \dot{x} \\ \dot{y} \end{bmatrix}=\begin{bmatrix} 0 & 1 \\ r \cos \phi & 0\\ r \sin \phi & 0 \end{bmatrix} \begin{bmatrix} u_1 \\ u_2 \\ \end{bmatrix} $$

$u = (u_1,u_2)$为控制输入，$u_1$为前后行驶时的转动速度，$u_2$为前进方向得到转速，其控制变换为

$$ u_1 = \frac{v}{r},\ u_2=w $$

其中

$$ w = \dot{\phi} $$

$$ \begin{aligned}
u_1^2 r^2({\cos \phi}^2+{\sin \phi}^2) &= \dot{x}^2+\dot{y}^2\\ u_1 &= \frac{\sqrt{\dot{x}^2+\dot{y}^2}}{r}\\ v &= \sqrt{\dot{x}^2+\dot{y}^2} \end{aligned} $$

差速模型（Differentially-drive）

两轮差速

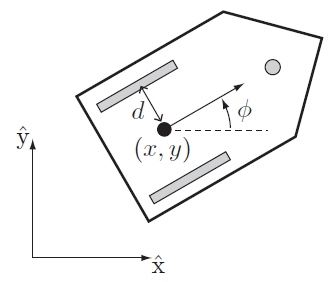
两轮差速机器人由两个独立驱动的半径为$r$轮子组成，围绕同一轴线旋转，并带有一个或多个脚轮、球形脚轮或使机器人保持水平的低摩擦滑块。

在实际应用中，车轮的组合可根据机器人对设计重心、转弯半径的要求，将辅助轮和驱动轮按照不同形式布置：

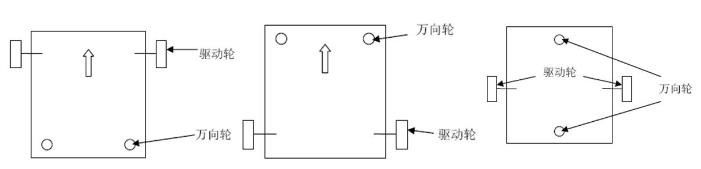
• 优点：结构及电机控制也相对简单，机器人灵活性较强，且算法易控制。
• 缺点：辅助轮（脚轮，万向轮）不适合在户外使用。

四轮差速

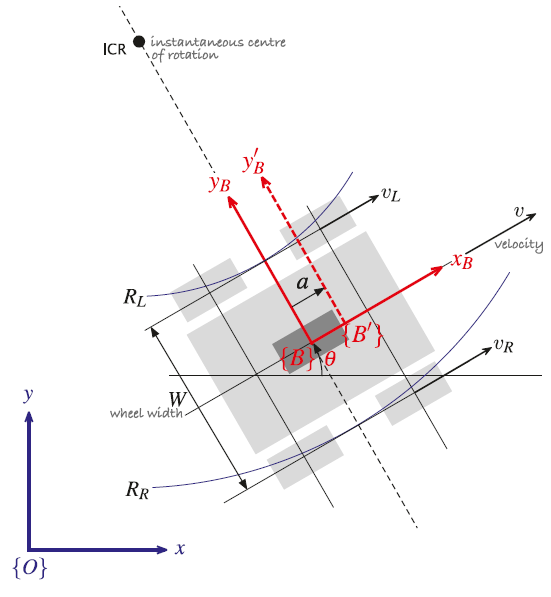
四轮差速车体为浅灰色外轮廓，可类似为深灰色的单轮模型，其运动学模型与两轮一样，因为同侧车轮转速相同。

四轮驱动在直线行走上能力较强，驱动力也比较大，但成本过高，电机控制较为复杂，为防止机器人打滑，需要更精细的结构设计。

小车车轮半径为$r$，左右轮角速度为$u = (u_L,u_R)$，线速度为

$$ \begin{matrix} v_L = r \cdot u_l \\ v_R = r \cdot u_R \end{matrix} $$

${B}$为小车的坐标系，其原点为小车的中心，X轴为小车前进方向，绕ICR旋转的角速度为：

$$ \dot{\theta} = \frac{v_L}{R_L} = \frac{v_R}{R_R} $$

因为$R_R = R_L +W$（$W$为左右两轮间距），因此$R_L$为：

$$ \begin{matrix} \frac{v_L}{R_L} = \frac{v_R}{R_L+W} \\ v_L \cdot R_L+v_L \cdot W = v_R \cdot R_L\\ R_L = \frac{v_L \cdot W}{v_R-v_L} \end{matrix} $$

将$R_L$带入方程可求得角速度（小车坐标系${B}$相对于世界坐标系${O}$）为：

$$ \dot{\theta} = \frac{v_R-v_L}{W} $$

小车的线速度为：

$$ v = \frac{v_R+v_L}{2} $$

小车的运动方程为：

$$ \begin{matrix} \dot{x} = v \cos{\theta} \\ \dot{y} = v \sin{\theta} \\ \dot{\theta} = \frac{v_R-v_L}{W} \end{matrix} $$

规范简化模型为：

$$ \dot{q}= \begin{bmatrix} \dot{\theta}\\ \dot{x}\\ \dot{y} \end{bmatrix}=\begin{bmatrix} -\frac{r}{w} & \frac{r}{w}\\ \frac{r}{2} \cos \theta & \frac{r}{2} \cos \theta\\ \frac{r}{2} \sin \theta & \frac{r}{2} \sin \theta\\ \end{bmatrix} \begin{bmatrix} u_L\\ u_R \end{bmatrix} $$

差速模型可以原地旋转，但不代表其为完整约束，本质上小车只有X轴移动和旋转两个控制自由量。

设$w = \dot{\theta},d = \frac{W}{2}$，小车的控制变换为：

$$ u_L= \frac{v-wd}{r},\ u_R= \frac{v+wd}{r} $$

$wd$为旋转时在离旋转中心$d$距离处产生的切向线速度，$v-wd$和$v+wd$为切向加上角速度产生的线速度的影响后的实际速度，其正负与固定在小车上的坐标系有关。

若将小车的参考系移动到${B^{’}}$并忽略旋转，运动方程可写为：

$$ \begin{pmatrix} \dot{x}\\dot{y} \end{pmatrix} = \begin{pmatrix} \cos{\theta} & -a \sin{\theta}\\ \sin{\theta} & a \cos{\theta} \end{pmatrix} \begin{pmatrix} v\\ w \end{pmatrix} $$

$w$为小车绕坐标系${B}$原点旋转的角速度，$a$为坐标系${B^{’}}$相对于${B}$在X轴方向上的移动，若$a \neq 0$，求逆后为：

$$ \begin{pmatrix} v\ w \end{pmatrix}=\begin{pmatrix} \cos{\theta} & \sin{\theta}\\ -\frac{1}{a}\sin{\theta} & \frac{1}{a} \cos{\theta} \end{pmatrix} \begin{pmatrix} \dot{x}\\ \dot{y} \end{pmatrix} $$

通过上式可以计算达到给定的线速度和角速度所需的X轴和Y轴方向的速度，可用于轨迹跟踪。

旋转运动分析

运动状态

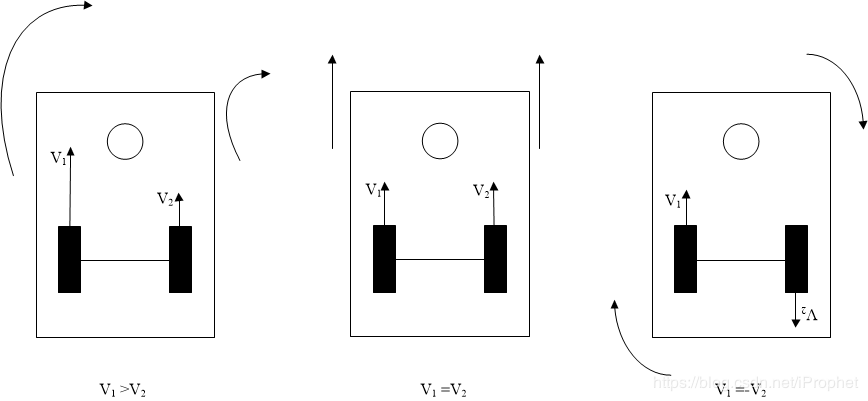
• 当$v_l > v_r || v_l < v_r$时，机器做圆弧运动；
• $v_l = v_r $时，机器做直线运动；
• 当$v_l =- v_r$时，机器以左右轮中心点做原地旋转；

力分析

1. 原地旋转

   差速模型在转动时，作用在车子上的为一对等大，方向相反的力，称为力偶。

   由两个等值、反向、不共线的（平行）力组成的力系称为力偶，记作$(\vec{F},\vec{F}^{,})$

   • 力偶中两力所在平面称为力偶作用面

   • 力偶两力之间的垂直距离称为力偶臂

   力偶在小车上形成一个力偶矩 $$ M = \pm F \cdot d $$

​ 力矩 = 转动惯量 x 角加速，力偶矩带动小车旋转。

2. 圆弧运动

   当作用小车两侧速度不一致时，在小车上产生一个力偶和沿小车前进方向的力，使其旋转的同时前进产生圆弧运动。

汽车模型（Car-Like Mobile）

汽车控制输入为$a$油门（前后加速度）和方向盘$\delta_f$（前轮转向）

运动学模型

该模型也称为双轮自行车模型，常被误称为阿克曼（Ackeman）模型，因为汽车的转向使用阿克曼转向几何。

使用阿克曼转向的汽车，在转向时，两个前轮的转向角不同，使得所有车轮做无滑动的纯滚动（即车轮前进方向垂直于车轮于ICR之间的连线）

控制点的设置会影响控制效果，可选控制点：

• 后轴中心
• 车辆质心
• 前轴中心

按车辆后轴中心建立模型

此处将车辆的后轴中心速度作为速度状态量，假设侧偏角$\beta$近似为0，即侧向速度为0。

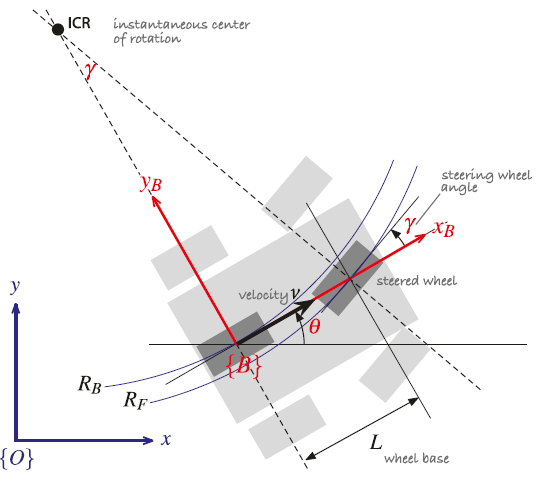
${O}$为世界坐标系。

${B}$为小车的坐标系，其原点为小车的后轮中心，X轴为小车前进方向，Y轴垂直于两轮中心线，在该坐标系下的小车速度为： $$ ^{B}V_x=v,^{B}V_y=0 $$ 虚线的交点为旋转瞬心（ICR），小车上的参考点（${B}$的原心）将绕该瞬心做圆弧运动，$\theta$为前进方向，其角速度为： $$ \begin{matrix} \dot{\theta} = \frac{u}{R_B}\\ R_B = \frac{L}{\tan{\gamma}} \end{matrix} $$ $R_B$为以ICR为原点的转弯半径，$\gamma$为前轮转向角度。

小车的运动模型为 $$ \begin{matrix} \dot{x} = u \cos\theta\\ \dot{y} = u \sin\theta\\ \dot{\theta} = \frac{u}{L}\tan \gamma \end{matrix} $$ 考虑前轮转角角速度时，小车状态空间为$X=(\theta,x,y,\gamma)$ $$ \begin{bmatrix} \dot{\theta}\\ \dot{x}\\ \dot{y}\\ \dot{\gamma} \end{bmatrix}= \begin{bmatrix} \frac{\tan \gamma}{L}&0\\ \cos \theta&0\\ \sin \theta&0\\ 0&1 \end{bmatrix} \begin{bmatrix} v\\ w\\ \end{bmatrix} $$ 在当前条件下，$v$为汽车前进速度，$w$为前轮角速度。

若转向控制为转向角$\gamma$而不是其速率$\dot{\gamma}$，则可以简化运动方程，其规范简化模型为：

当转向速率$\dot{\gamma}$足够高，使得转向角几乎为瞬时改变，则该假设合理，在这种情况下，$\dot{\gamma}$作为状态变量被消除，小车状态空间为$X=(\theta,x,y)$

$$ \begin{bmatrix} \dot{\theta} \\ \dot{x} \\ \dot{y} \end{bmatrix}= \begin{bmatrix} 0&1 \\ \cos \theta & 0 \\ \sin \theta & 0 \end{bmatrix} \begin{bmatrix} v\\ w\\ \end{bmatrix} $$

在当前条件下，$v$为汽车前进速度，$w$为汽车角速度。

根据控制输出 $(v,\gamma)$，其控制变换为： $$ \begin{matrix} v = v\ \gamma = \tan^{-1}(\frac{Lw}{v}) \end{matrix} $$

运动学模型线性化

在$X_r = [x_r,y_r,\theta_r]^T,u_r=[v_r,\gamma]^T$进行一阶泰勒展开

在世界坐标系${O}$中，Y方向的速度约束为：

$\equiv$为恒等号，参变量恒为一个常数或恒定表达式时，总等于关系与变量无关。例如函数$f(x)\equiv k$表示该函数的值始终为k而与x的值无关。

$$ ^{O}V_y \cos{\theta} - ^{O}V_x \sin{\theta} \equiv 0 $$

根据不同情况，该模型存在不同的约束

• simple car model

  $$ |v| \leqslant v_{max}, |\theta| \leqslant \theta_{max} < \frac{\pi}{2} $$

• Reeds & Shepp’s car（前进、后退和停止）

  $$ v \in {-v_{max},v_{max} }, |\theta| \leqslant \theta_{max} < \frac{\pi}{2} $$

• Dubin’s car（前进和停止）

  $$ v = v_{max}, |\theta| \leqslant \theta_{max} < \frac{\pi}{2} $$

按车辆质心建立模型

此处车辆侧向速度不为0

此处使用四个状态量来描述车辆的当前状态：

• $x$：车辆当前的$x$坐标
• $y$：车辆当前的$y$坐标
• $\psi$：车辆当前的偏航角（逆时针方向为正）
• $v$：车辆的速度

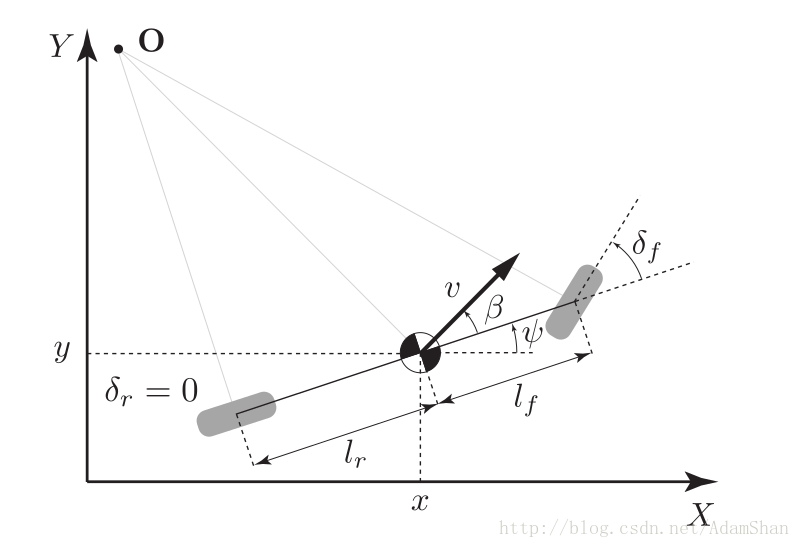
运动模型

$$ \begin{matrix} \dot{X}=v\cos \left( \varphi +\beta \right)\\ \dot{Y}=v\sin \left( \varphi +\beta \right)\\ \dot{\varphi}=\frac{v\sin \left( \beta \right)}{l_r} \end{matrix} $$

其中$l_f$和$l_r$为前轮和后轮到车辆重心的距离，状态更新如下：

$$ \begin{matrix} x_{t+1} = x_t + v_t\cos(\psi_t + \beta) \times dt \\ y_{t+1} = y_t + v_t\sin(\psi_t + \beta) \times dt \\ \psi_{t+1} = \psi_t + \frac{v_t}{l_r}\sin(\beta) \times dt \\ v_{t+1} = v_t + a \times dt \end{matrix} $$

$\beta$为车辆的质心侧偏角，计算如下：

$$ \beta = \tan^{-1} \left( \frac{l_r}{l_f + l_r} \tan \left( \delta_f \right)\right) $$

Python实现

import math

class KinematicModel(object):
    def __init__(self, x, y, psi, v, f_len, r_len):
        self.x = x
        self.y = y
        self.psi = psi
        self.v = v

        self.f_len = f_len
        self.r_len = r_len

    def get_state(self):
        return self.x, self.y, self.psi, self.v

    def update_state(self, a, delta, dt):
        beta = math.atan((self.r_len / (self.r_len + self.f_len)) * math.tan(delta))

        self.x = self.x + self.v * math.cos(self.psi * beta) * dt
        self.y = self.y + self.v * math.sin(self.psi * beta) * dt
        self.psi = self.psi + (self.v / self.f_len) * math.sin(beta) * dt
        self.v = self.v + a * dt
        return self.x, self.y, self.psi, self.v

动力学模型

自行车模型隐含着一个重要的假设：车前轮的方向即是车辆当前的速度方向，在实际车辆运动过程中，当车辆在以相对高的速度行驶时，车轮的方向并不一定车辆当前的速度方向，这个时候需要引入车辆的动力学自行车模型。

车辆动力学模型通过对轮胎和路面之间的复杂相互作用来描述车辆的运动。在一个动力模型中，我们需要考虑各种各样的力的作用，他们可以大致分为两类：纵向力（Longitudinal force）和侧向力（Lateral force）, 纵向力就是使车辆前后移动的力量，而侧向力则促使车辆在横向移动，在力的相互作用过程中，轮胎起着决定性的作用。

此处为一个简单的动力学模型，模型状态量为$(\dot{x},\dot{y},\dot{\psi},X,Y)$，其中$\dot{x},\dot{y}$为车身的纵向和侧向速度，$\dot{\psi}$为偏航角速度，$X,Y$为车身的当前坐标，这些状态量在时间尺度上的微分方程为：

$$ \ddot{x} =\dot{\psi} \cdot \dot{y} + a_x\ $$

其中，$m$和$I_z$分别表示车辆的质量和偏航惯性(yaw inertia)，$F_{c,f}$和$F_{c,r}$分别表示的是前后轮胎受到的侧向力，他们可以通过具体的轮胎模型求得，在简单的线性轮胎模型中：

$$ F_{c, i}(i=f/r) = -C_{\alpha_i}\alpha_i $$

其中$\alpha_i$是轮胎的偏转角，这个偏转角是指轮胎当前的朝向和当前的速度的夹角，$C_{\alpha_i}$为轮胎偏滚刚度（tire cornering stiffness）。

全向轮模型（Omnidirectional Vehicle）

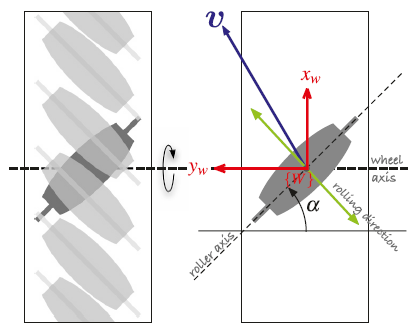
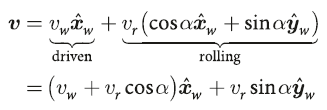
$$ v_w = v_x-v_y \cot \alpha $$

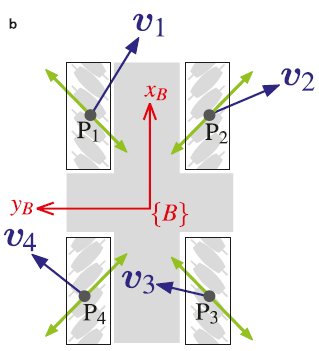
$$ ^{B}v_{i} = ^{B}v_{B}+^{B}w \hat{z}_B \times ^{B}P_i $$

参考

《Robotics, Vision and Control: Fundamental Algorithms in MATLAB Second Edition》——4 Mobile Robot Vehicles

《现代机器人学：机构、规划与控制》——13 轮式移动机器人

Kinematics for Wheeled Systems

图解差速机器人的三种运动学模型

两轮差速移动机器人运动分析、建模和控制

无人驾驶汽车系统入门（五）——运动学自行车模型和动力学自行车模型

无人车系统（一）：运动学模型及其线性化

• Next Post →